1.问题的发现与定位
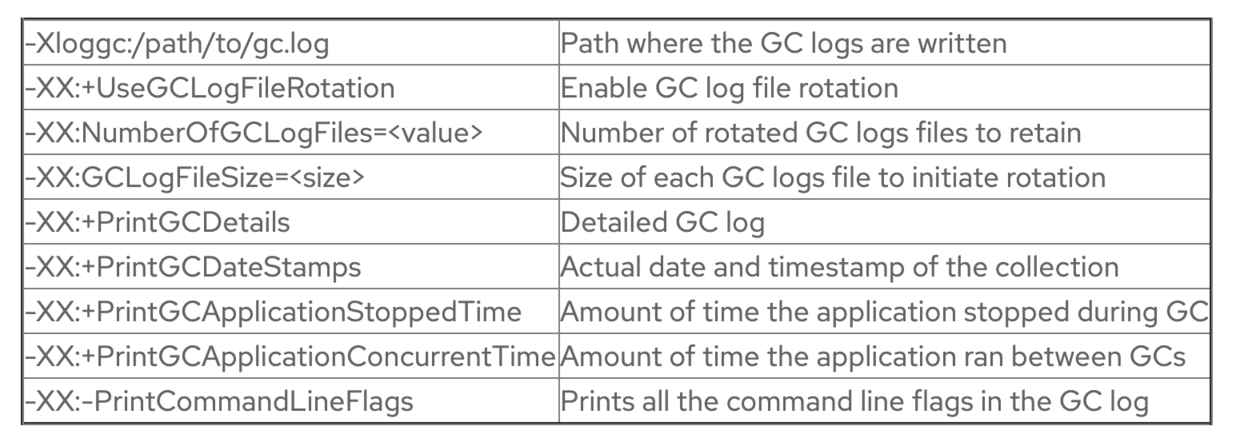
1.1统计nginx每秒中流量时发现轮询到每台机器上的流量不均衡,找到后端机器,看gc 日志发现出现大量的full gc,对比gc时间和流量统计的时间,发现时间是完全吻合的,从而定位流量不均衡问题是因为线上服务full gc引起的。
2019-08-30T11:33:06.130+0800: 780570.463: [GC pause (G1 Evacuation Pause) (young)2019-08-30T11:33:06.352+0800: 780570.685: [SoftReference, 0 refs, 0.0000547 secs]2019-08-30T11:33:06.352+0800: 780570.685: [WeakReference, 0 refs, 0.0000128 secs]2019-08-30T11:33:06.352+0800: 780570.685: [FinalReference, 0 refs, 0.0000103 secs]2019-08-30T11:33:06.352+0800: 780570.685: [PhantomReference, 0 refs, 0 refs, 0.0000147 secs]2019-08-30T11:33:06.352+0800: 780570.685: [JNI Weak Reference, 0.0000183 secs] (to-space exhausted), 0.2410054 secs]
[Parallel Time: 212.0 ms, GC Workers: 23]
[GC Worker Start (ms): Min: 780570465.3, Avg: 780570465.5, Max: 780570465.9, Diff: 0.6]
[Ext Root Scanning (ms): Min: 0.4, Avg: 0.8, Max: 2.2, Diff: 1.9, Sum: 18.4]
[Update RS (ms): Min: 33.8, Avg: 37.4, Max: 40.3, Diff: 6.4, Sum: 861.1]
[Processed Buffers: Min: 9, Avg: 30.3, Max: 137, Diff: 128, Sum: 697]
[Scan RS (ms): Min: 0.0, Avg: 0.0, Max: 0.0, Diff: 0.0, Sum: 0.0]
[Code Root Scanning (ms): Min: 0.0, Avg: 0.0, Max: 0.0, Diff: 0.0, Sum: 0.0]
[Object Copy (ms): Min: 169.7, Avg: 173.0, Max: 176.7, Diff: 7.0, Sum: 3979.6]
[Termination (ms): Min: 0.0, Avg: 0.3, Max: 0.4, Diff: 0.4, Sum: 5.8]
[Termination Attempts: Min: 1, Avg: 1.3, Max: 3, Diff: 2, Sum: 30]
[GC Worker Other (ms): Min: 0.0, Avg: 0.0, Max: 0.4, Diff: 0.4, Sum: 0.8]
[GC Worker Total (ms): Min: 211.2, Avg: 211.6, Max: 211.8, Diff: 0.7, Sum: 4865.7]
[GC Worker End (ms): Min: 780570677.0, Avg: 780570677.1, Max: 780570677.1, Diff: 0.0]
[Code Root Fixup: 0.0 ms]
[Code Root Purge: 0.0 ms]
[Clear CT: 0.2 ms]
[Other: 28.8 ms]
[Evacuation Failure: 18.1 ms]
[Choose CSet: 0.0 ms]
[Ref Proc: 7.5 ms]
[Ref Enq: 0.0 ms]
[Redirty Cards: 0.4 ms]
[Humongous Register: 1.5 ms]
[Humongous Reclaim: 0.2 ms]
[Free CSet: 0.1 ms]
[Eden: 44.0M(6116.0M)->0.0B(6144.0M) Survivors: 28.0M->0.0B Heap: 9482.2M(12.0G)->9482.2M(12.0G)]
Heap after GC invocations=266041 (full 14579):
garbage-first heap total 12582912K, used 9709773K [0x00000004c0000000, 0x00000004c0406000, 0x00000007c0000000)
region size 4096K, 0 young (0K), 0 survivors (0K)
Metaspace used 59825K, capacity 60428K, committed 62016K, reserved 1103872K
class space used 6597K, capacity 6776K, committed 7056K, reserved 1048576K
}
[Times: user=0.57 sys=0.08, real=0.24 secs]
2019-08-30T11:33:06.372+0800: 780570.705: Total time for which application threads were stopped: 0.2499226 seconds, Stopping threads took: 0.0007422 seconds
{Heap before GC invocations=266041 (full 14579):
garbage-first heap total 12582912K, used 9709773K [0x00000004c0000000, 0x00000004c0406000, 0x00000007c0000000)
region size 4096K, 0 young (0K), 0 survivors (0K)
Metaspace used 59825K, capacity 60428K, committed 62016K, reserved 1103872K
class space used 6597K, capacity 6776K, committed 7056K, reserved 1048576K
2019-08-30T11:33:06.380+0800: 780570.712: [GC pause (G1 Evacuation Pause) (young) (initial-mark)2019-08-30T11:33:06.392+0800: 780570.725: [SoftReference, 0 refs, 0.0000740 secs]2019-08-30T11:33:06.392+0800: 780570.725: [WeakReference, 0 refs, 0.0000127 secs]2019-08-30T11:33:06.392+0800: 780570.725: [FinalReference, 0 refs, 0.0000103 secs]2019-08-30T11:33:06.392+0800: 780570.725: [PhantomReference, 0 refs, 0 refs, 0.0000147 secs]2019-08-30T11:33:06.392+0800: 780570.725: [JNI Weak Reference, 0.0000174 secs], 0.0144402 secs]
[Parallel Time: 10.2 ms, GC Workers: 23]
[GC Worker Start (ms): Min: 780570714.5, Avg: 780570715.2, Max: 780570716.2, Diff: 1.7]
[Ext Root Scanning (ms): Min: 1.1, Avg: 1.9, Max: 2.8, Diff: 1.7, Sum: 44.1]
[Update RS (ms): Min: 6.1, Avg: 6.5, Max: 7.3, Diff: 1.2, Sum: 150.3]
[Processed Buffers: Min: 3, Avg: 9.9, Max: 18, Diff: 15, Sum: 227]
[Scan RS (ms): Min: 0.0, Avg: 0.0, Max: 0.0, Diff: 0.0, Sum: 0.0]
[Code Root Scanning (ms): Min: 0.0, Avg: 0.0, Max: 0.0, Diff: 0.0, Sum: 0.0]
[Object Copy (ms): Min: 0.0, Avg: 0.2, Max: 0.4, Diff: 0.4, Sum: 4.7]
[Termination (ms): Min: 0.0, Avg: 0.5, Max: 0.7, Diff: 0.7, Sum: 12.5]
[Termination Attempts: Min: 1, Avg: 1.0, Max: 1, Diff: 0, Sum: 23]
[GC Worker Other (ms): Min: 0.0, Avg: 0.0, Max: 0.0, Diff: 0.0, Sum: 0.3]
[GC Worker Total (ms): Min: 8.3, Avg: 9.2, Max: 10.0, Diff: 1.7, Sum: 211.9]
[GC Worker End (ms): Min: 780570724.4, Avg: 780570724.4, Max: 780570724.4, Diff: 0.0]
[Code Root Fixup: 0.0 ms]
[Code Root Purge: 0.0 ms]
[Clear CT: 0.3 ms]
[Other: 3.9 ms]
[Choose CSet: 0.0 ms]
[Ref Proc: 0.7 ms]
[Ref Enq: 0.0 ms]
[Redirty Cards: 0.3 ms]
[Humongous Register: 1.4 ms]
[Humongous Reclaim: 0.2 ms]
[Free CSet: 0.0 ms]
[Eden: 0.0B(6144.0M)->0.0B(6144.0M) Survivors: 0.0B->0.0B Heap: 9482.2M(12.0G)->9482.2M(12.0G)]
Heap after GC invocations=266042 (full 14579):
garbage-first heap total 12582912K, used 9709773K [0x00000004c0000000, 0x00000004c0406000, 0x00000007c0000000)
region size 4096K, 0 young (0K), 0 survivors (0K)
Metaspace used 59825K, capacity 60428K, committed 62016K, reserved 1103872K
class space used 6597K, capacity 6776K, committed 7056K, reserved 1048576K
}
[Times: user=0.13 sys=0.01, real=0.02 secs]
2019-08-30T11:33:06.394+0800: 780570.727: [GC concurrent-root-region-scan-start]
2019-08-30T11:33:06.394+0800: 780570.727: [GC concurrent-root-region-scan-end, 0.0000314 secs]
2019-08-30T11:33:06.394+0800: 780570.727: [GC concurrent-mark-start]
2019-08-30T11:33:06.394+0800: 780570.727: Total time for which application threads were stopped: 0.0225686 seconds, Stopping threads took: 0.0003015 seconds
{Heap before GC invocations=266042 (full 14579):
garbage-first heap total 12582912K, used 9709773K [0x00000004c0000000, 0x00000004c0406000, 0x00000007c0000000)
region size 4096K, 0 young (0K), 0 survivors (0K)
Metaspace used 59825K, capacity 60428K, committed 62016K, reserved 1103872K
class space used 6597K, capacity 6776K, committed 7056K, reserved 1048576K
2019-08-30T11:33:06.402+0800: 780570.735: [Full GC (Allocation Failure) 2019-08-30T11:33:06.812+0800: 780571.145: [SoftReference, 155 refs, 0.0000827 secs]2019-08-30T11:33:06.812+0800: 780571.145: [WeakReference, 4919 refs, 0.0004444 secs]2019-08-30T11:33:06.812+0800: 780571.145: [FinalReference, 38797 refs, 0.0256226 secs]2019-08-30T11:33:06.838+0800: 780571.171: [PhantomReference, 0 refs, 4 refs, 0.0000267 secs]2019-08-30T11:33:06.838+0800: 780571.171: [JNI Weak Reference, 0.0000255 secs] 9482M->3317M(12G), 1.3316541 secs]
[Eden: 0.0B(6144.0M)->0.0B(6144.0M) Survivors: 0.0B->0.0B Heap: 9482.2M(12.0G)->3317.3M(12.0G)], [Metaspace: 59825K->59825K(1103872K)]
Heap after GC invocations=266043 (full 14580):
garbage-first heap total 12582912K, used 3396899K [0x00000004c0000000, 0x00000004c0406000, 0x00000007c0000000)
region size 4096K, 0 young (0K), 0 survivors (0K)
Metaspace used 59825K, capacity 60428K, committed 62016K, reserved 1103872K
class space used 6597K, capacity 6776K, committed 7056K, reserved 1048576K
}
[Times: user=1.83 sys=0.12, real=1.34 secs]
2 问题分析与处理
2.1 分析日志发现在新生代回收时触发了老年代的担保机制,导致新生代对象直接晋升到了老年代,然后触发并发周期,这时由于老年代对象太多已经不足以触发mixed GC,而是采用了最耗时的Full GC进行垃圾回收,由于Full GC耗时很长导致,后续的新生代在垃圾回收时还是会触发老年代担保机制,从而整个程序陷入循环Full GC的状态。
2.2 根据to-space exhausted我们知道,调整空闲区域预留百分比是能缓解新生代垃圾回收空间溢出问题,我们尝试增加XX:G1ReservePercent=15;另外我们为了降低Full GC触发概率,减小了InitiatingHeapOccupancyPercent的大小,这样我们可以用更加频繁的mixed gc降低 full gc问题
2.3 根据G1的启发式算法,我们为了控制gc时间,决定放弃原有的gc用法,让g1决定新生代和老年代大小,我们删除了Xmn参数设置
2-4 在gc日志中我们也发现了大对象分配与回收的现象,考虑到我们线上视频大小,我们调整region大小到16M
3 观察对比后再次处理
3.1 通过上述调整对比观察四台机器,两天以后,原有的机器出现Full GC 调整后的机器运行正常
3.2 观察调整后日志发现新调整的gc没有出现Full gc,但是mixed gc问题出现频率在20min一次,这个频率出现理论上对整个gc的吞吐几乎没有影响,但是分析后会发现mixed gc回收效率很低,所以我们尝试改善mixed gc的效率
3.3 根据上述我们对InitiatingHeapOccupancyPercent参数的调整,我们根据线上观察到的老年代大小和新生代大小,调整值为50
3.4 对比观察后发现调整后mixed gc频率在流量高峰期间为2小时一次,流量低峰期间为6小时一次,并且mixed gc 回收效率大大提高
4.调优后效果
经过调优后线上没有触发 full gc, yang gc 和mixed gc 效率都很高,整个gc的吞吐达到 99%以上