之前说过CFS是Kernel中的一种调度policy,这个调度算法的核心,所有task都应该公平分配处理器,为了达成这个目标,CFS调度使用vruntime来衡量某一个进程是否值得调度。
上篇博文初步对CFS的实现有了一个说明,但是没有阐述vruntime的计算。
上篇 http://www.lizhaozhong.info/archives/1206
vruntime 是CFS算法模拟出来的一个变量,他淡化了优先级在调度中的作用,而是以vruntime的值使用struct sched_entity组织成为一棵red-black tree。
根据red-black tree的特点,值小的在tree的左边,值大的在右边,随着进程的运行,系统在timer 中断发生时会调用policy中的task_tick()方法,这个函数可以更新vruntime的值。以供CFS调度时使用。
为了维护这个red-black tree最左边的节点vruntime值最小,我们必须使得这个值单调递增,所以要比较delta_exec 与 curr->statistics.exec_max值的,并取最大值。schedstat_set(curr->statistics.exec_max,max(delta_exec, curr->statistics.exec_max));update_min_vruntime(cfs_rq);
通过这两个函数,只有最靠左的节点超过min_vruntime才会更新。
有一种情况,如果进程睡眠,则他的vruntime不变,而min_vruntime变大,则,这个进程会更加靠左!
调用路径是:
void scheduler_tick(void)
{... curr->sched_class->task_tick(rq, curr, 0); ...}
->通过函数指针,调用具体policy的函数,在CFS中是task_tick_fair,这个函数可以调用entity_tick()更新
当前调度实体sched_entity所在的cfs_rq中当前运行task的sche_entity中vruntime的值
->
3097 static void
3098 entity_tick(struct cfs_rq *cfs_rq, struct sched_entity *curr, int queued)
3099 {
3100 /*
3101 * Update run-time statistics of the 'current'.
3102 */
3103 update_curr(cfs_rq);
3104
......
3131 }
->static void update_curr(struct cfs_rq *cfs_rq)
从entity_tick()中的update_curr()调cfs中真正更新vruntime值的函数:
694 static void update_curr(struct cfs_rq *cfs_rq)
695 {
....
697 u64 now = rq_clock_task(rq_of(cfs_rq));
....
703 delta_exec = now - curr->exec_start;
704 if (unlikely((s64)delta_exec <= 0))
705 return;
706
707 curr->exec_start = now;
708
709 schedstat_set(curr->statistics.exec_max,
710 max(delta_exec, curr->statistics.exec_max));
711
712 curr->sum_exec_runtime += delta_exec;
713 schedstat_add(cfs_rq, exec_clock, delta_exec);
714
715 curr->vruntime += calc_delta_fair(delta_exec, curr);
716 update_min_vruntime(cfs_rq);
717
718 if (entity_is_task(curr)) {
719 struct task_struct *curtask = task_of(curr);
720
721 trace_sched_stat_runtime(curtask, delta_exec, curr->vruntime);
722 cpuacct_charge(curtask, delta_exec);
723 account_group_exec_runtime(curtask, delta_exec);
724 }
725
726 account_cfs_rq_runtime(cfs_rq, delta_exec);
727 }
首先获取当前rq的时间,使用delta_exec获取当前进程运行的实际时间,然后将exec_start再次更新为now以便下一次使用。
并将该值加到sum_exec_runtime中时间中,对于vruntime 时间则需要calc_delta_fair(delta_exec, curr);进行处理。
通过下表我们可以看出当nice值为0,weight值为1024。另外我们需要明确nice值【-20,+19】映射到整个系统中是100~139,也就是说nice值每增加一个nice值,获得cpu时间减少10%,反之增加10%!而0~99则属于实时进程专用!nice值越高权值越小!
1046 static const int prio_to_weight[40] = {
1047 /* -20 */ 88761, 71755, 56483, 46273, 36291,
1048 /* -15 */ 29154, 23254, 18705, 14949, 11916,
1049 /* -10 */ 9548, 7620, 6100, 4904, 3906,
1050 /* -5 */ 3121, 2501, 1991, 1586, 1277,
1051 /* 0 */ 1024, 820, 655, 526, 423,
1052 /* 5 */ 335, 272, 215, 172, 137,
1053 /* 10 */ 110, 87, 70, 56, 45,
1054 /* 15 */ 36, 29, 23, 18, 15,
1055 };
在calc_delta_fair()函数中会比较当前权重与nice值为0的权重(NICE_0_LOAD),如果等于则直接返回加权后的vruntime,如果不同则需要对该权值加权。
struct sched_entity *se 存在着当前进程的权重,就是上面那个array里面数字!
601 static inline u64 calc_delta_fair(u64 delta, struct sched_entity *se)
602 {
603 if (unlikely(se->load.weight != NICE_0_LOAD))
604 delta = __calc_delta(delta, NICE_0_LOAD, &se->load);
605
606 return delta;
607 }
如果当前进程的nice值不等于nice 0 ,进入下面的函数:
214 static u64 __calc_delta(u64 delta_exec, unsigned long weight, struct load_weight *lw)
215 {
216 u64 fact = scale_load_down(weight);
217 int shift = WMULT_SHIFT;
218
219 __update_inv_weight(lw);
220
221 if (unlikely(fact >> 32)) {
222 while (fact >> 32) {
223 fact >>= 1;
224 shift--;
225 }
226 }
227
228 /* hint to use a 32x32->64 mul */
229 fact = (u64)(u32)fact * lw->inv_weight;
230
231 while (fact >> 32) {
232 fact >>= 1;
233 shift--;
234 }
235
236 return mul_u64_u32_shr(delta_exec, fact, shift);
237 }
这个函数有些复杂,我现在理解这个加权公式就是delta_exec = delta_exec * (weight / lw.weight)
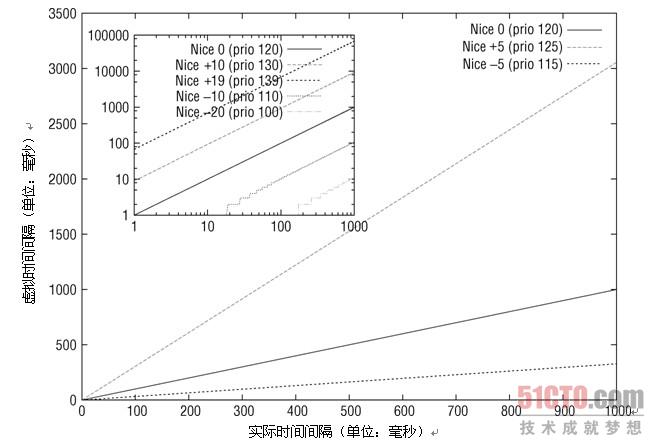
我们可以绘制出不同nice下,加权后vruntime与真实的delta_exec值的关系。我们可以对照上面那个数组发现nice值越高,权值越小,在这里我们比较的是1024/lw.weight的值,权值越小的,商越大,vruntime越大!在CFS中,vruntime值越小,越容易调度!
mul_u64_u32_shr()函数应该是32位与64位转换的,具体没研究清楚,改天再来。
具体这个的解释:
/*
203 * delta_exec * weight / lw.weight
204 * OR
205 * (delta_exec * (weight * lw->inv_weight)) >> WMULT_SHIFT
206 *
207 * Either weight := NICE_0_LOAD and lw \e prio_to_wmult[], in which case
208 * we're guaranteed shift stays positive because inv_weight is guaranteed to
209 * fit 32 bits, and NICE_0_LOAD gives another 10 bits; therefore shift >= 22.
210 *
211 * Or, weight =< lw.weight (because lw.weight is the runqueue weight), thus
212 * weight/lw.weight <= 1, and therefore our shift will also be positive.
213 */
CFS总结:
1)不再区分进程类型,不使用nice值判断优先级,而是使用vruntime衡量一个进程的重要性。
2)对于IO类型的进程,随着睡眠时间正常,仍然可以得到公平的时间片
3)对于优先级高的进程,可以获得更多的CPU时间。
参考:
http://lxr.free-electrons.com/source/kernel/sched/fair.c#L214
http://lxr.free-electrons.com/source/kernel/sched/sched.h#L1046