回归模型中线性回归是最最基本的模型,也是在数据处理中运用最多的模型。sklearn提供了一套完备的工具集,可以对数据进行拟合和预测。
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression,RidgeCV,LassoCV,ElaticNetCV
from sklearn.preprocessing.PolynomialFeatures import PolynomialFeatures
models = [Pipeline([
('poly', PolynomialFeatures()),
('linear', LinearRegression(fit_intercept=False))]),
Pipeline([
('poly', PolynomialFeatures()),
('linear', RidgeCV(alphas=np.logspace(-3, 2, 50), fit_intercept=False))]),
Pipeline([
('poly', PolynomialFeatures()),
('linear', LassoCV(alphas=np.logspace(-3, 2, 50), fit_intercept=False))]),
Pipeline([
('poly', PolynomialFeatures()),
('linear', ElasticNetCV(alphas=np.logspace(-3, 2, 50), l1_ratio=[.1, .5, .7, .9, .95, .99, 1],
fit_intercept=False))])
]
模型中的fit_intercept代表是否存在截距,默认是开启的,normalize:标准化开关,默认关闭。
通过上面的头文件就可以看出来除了提供最最基本的LinearRegression以外,还提供带有L1 L2范数的LassoCV和RidgeCV。
LinearRegression的损失函数为J(θ)=1/2(Xθ−Y)T(Xθ−Y) 。优化方法为梯度下降和最小二乘法,scikit中采用最小二乘
。只要数据线性相关,LinearRegression就是首选,如果发现拟合或者预测的不够好,再考虑其他的线性回归库。
LassoCV的损失函数为J(θ)=1/2m(Xθ−Y)T(Xθ−Y)+α||θ|| 。即 线性回归LineaRegression的损失函数+L1(1范式的正则化项α||θ||) ,Lasso回归可以使得一些特征的系数变小,甚至还使一些绝对值较小的系数直接变为0,从而增强模型的泛化能力,因此对于高维的特征数据,尤其是线性关系是稀疏的,就采用Lasso回归,或者是要在一堆特征里面找出主要的特征。
RidgeCV的损失函数为J(θ)=1/2(Xθ−Y)T(Xθ−Y)+1/2(α||θ||^2)。即线性回归LineaRegression的损失函数+L2(2范式的正则化项1/2(α||θ||^2))),其中a为超参数 alphas=np.logspace(-3, 2, 50) 从给定的超参数a中选择一个最优的,logspace用于创建等比数列 本例中 开始点为10的-3次幂,结束点10的2次幂,元素个数为50.并且从这50个数中选择一个最优的超参数。Ridge回归中超参数a和回归系数θ的关系,a越大,正则项惩罚的就越厉害,得到的回归系数θ就越小,最终趋近与0。如果a越小,即正则化项越小,那么回归系数θ就越来越接近于普通的线性回归系数。
#使用场景:只要数据线性相关,用LinearRegression拟合的不是很好,需要正则化,可以考虑使用RidgeCV回归。
ElaticNetCV的损失函数为J(θ)=1/2m(Xθ−Y)T(Xθ−Y)+αρ||θ||1+α(1−ρ)/2||θ||22 其中α为正则化超参数,ρ为范数权重超参数 。乍一看就是Lasso和Ridge损失函数的合体。其中alphas=np.logspace(-3, 2, 50), l1_ratio=[.1, .5, .7, .9, .95, .99, 1] 。ElasticNetCV会从中选出最优的 a和p 。ElasticNetCV类对超参数a和p使用交叉验证,帮助选择合适的a和p,使用场景:ElasticNetCV类在我们发现用Lasso回归太过(太多特征被稀疏为0),而Ridge回归也正则化的不够(回归系数衰减太慢)的时候。
所以综上排名:LinearRegression > LassoCV(稀疏) > ElaticNetCV > RidgeCV(稠密)
model = models[t]
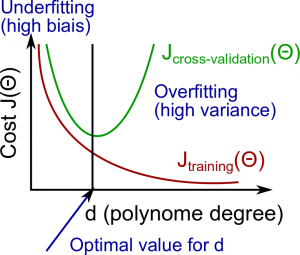
model.set_params(poly__degree=d) #设置多项式回归的阶
model.fit(x, y.ravel())
lin = model.get_params('linear')['linear']
if hasattr(lin, 'alpha_'):
...
if hasattr(lin, 'l1_ratio_'): # 根据交叉验证结果,从输入l1_ratio(list)中选择的最优l1_ratio_(float)
...
print output, lin.coef_.ravel(),lin.intercept_
y_hat = model.predict(x_hat)
s = model.score(x, y)
sklearn中提供了pipeline,只要把模型定义好,就可以直接利用fit对数据进行拟合,拟合完毕后使用predict进行预测。其中通过get_params可以获取某个模型,然后就能访问该回归模型的coef_和intercept_ ,如果模型设置的fit_intercept=false,那么打印出的lin.coef_中第一项就是截距,后面的为各个相关系数,lin.intercept_为0。如果置为true,那么lin.intercept_为截距值。
model.score主要用来衡量模型的拟合程度,Returns the coefficient of determination R^2 of the prediction.
R^2就是1-RSS/TSS,R^2越大,拟合效果越好。如果预测值为样本期望,那么R^2为0。
附sklearn工具类
| 包 | 类 | 参数列表 | 类别 | fit方法有用 | 说明 |
| sklearn.preprocessing | StandardScaler | 特征 | 无监督 | Y | 标准化 |
| sklearn.preprocessing | MinMaxScaler | 特征 | 无监督 | Y | 区间缩放 |
| sklearn.preprocessing | Normalizer | 特征 | 无信息 | N | 归一化 |
| sklearn.preprocessing | Binarizer | 特征 | 无信息 | N | 定量特征二值化 |
| sklearn.preprocessing | OneHotEncoder | 特征 | 无监督 | Y | 定性特征编码 |
| sklearn.preprocessing | Imputer | 特征 | 无监督 | Y | 缺失值计算 |
| sklearn.preprocessing | PolynomialFeatures | 特征 | 无信息 | N | 多项式变换(fit方法仅仅生成了多项式的表达式) |
| sklearn.preprocessing | FunctionTransformer | 特征 | 无信息 | N | 自定义函数变换(自定义函数在transform方法中调用) |
| sklearn.feature_selection | VarianceThreshold | 特征 | 无监督 | Y | 方差选择法 |
| sklearn.feature_selection | SelectKBest | 特征/特征+目标值 | 无监督/有监督 | Y | 自定义特征评分选择法 |
| sklearn.feature_selection | SelectKBest+chi2 | 特征+目标值 | 有监督 | Y | 卡方检验选择法 |
| sklearn.feature_selection | RFE | 特征+目标值 | 有监督 | Y | 递归特征消除法 |
| sklearn.feature_selection | SelectFromModel | 特征+目标值 | 有监督 | Y | 自定义模型训练选择法 |
| sklearn.decomposition | PCA | 特征 | 无监督 | Y | PCA降维 |
| sklearn.lda | LDA | 特征+目标值 | 有监督 | Y | LDA降维 |
参考
http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.RidgeCV.html