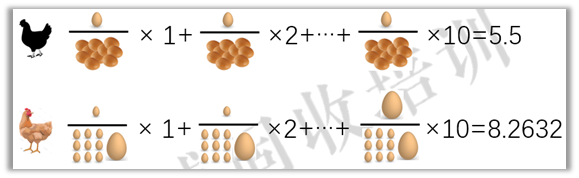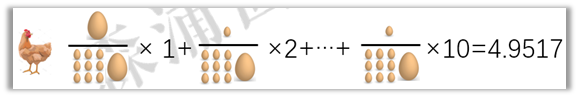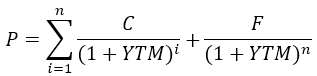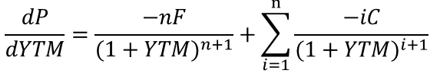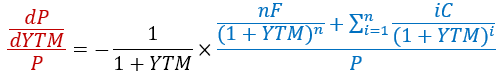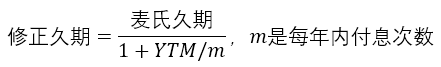1、在固收语境里,利率、收益率、贴现率,三者可以互相替代。收益率就是利率,也是贴现率,反之亦然。离开固收,这个替代关系不成立。
2、贴现是计息的逆过程。把较晚时点的现金、资产等价值物的价格折算到较早时点,称为贴现,不局限于折算到今天。去年折算到前年、明年折算到今年、后年折算到明年,都是贴现。贴现的英文是discount,所以我们一直认为把贴现翻译成‘折算’更合理。
3、债券到期收益率:假设投资者买入一只债券并能顺利持有到期的年化收益率,就是债券的到期收益率(Yield To Maturity,以下简称YTM)
这是一个基于如下假设条件的收益率:
- 发行人按时按量支付本息至债券到期。
- 持有人生存并持有债券至到期。
- 年化,而不是半年度化、季度化。年化的本质是平均,也就是把各年的收益率都平均成一个均值。
- 对于债券定价,一年以上通常是复利贴现,一年及以下通常是单利贴现(衍生品另议),因为年化复利的意思就是计息间隔为年,年以下无复利只有单利。
- 持有人将收到的每一期票息,都能按照YTM的复利再投资直至到期。
买债券就是用今天的现金流支出换未来的一系列现金流收入,所以定价的思路就是‘未来现金流今天值多少钱’,即贴现。
面值×票息率=每期票息金额。固息债的票息率不变,浮息债现在无法确定每期票息率,每次付息前一段时间(如提前1天、5天等)再确定下期票息。
前文提到,既然买债券是现在的现金流支出换未来现金流收入,那么其收益率也就可以类似看成付出资金的回报利率了,这也是为什么固收语境下,收益率就是利率。所以,如果你在研报、新闻里看到“XX债券的利率”,通常是指它的YTM,而不是票息率。只有明确提到票面利率、票息(率)、息票(率)、Coupon (Rate)时,才是指票面利率。这在英文固收语境里没有歧义,到期收益率会写清楚是Yield To Maturity, Yield, Redemption Yield(英国人喜欢这么说), Book Yield。票息率会写清楚是Coupon Rate。中文的‘债券利率’容易有误会或歧义,注意辨析。
4、首先要用业务逻辑理解业务,其次才是数学逻辑
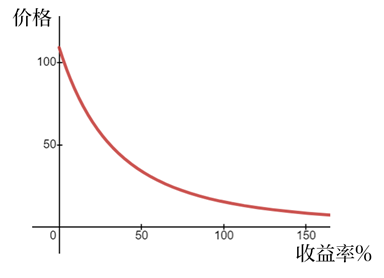
由于YTM在定价公式的分母,分子是固定的票息和本金,那么YTM越高,债券价格必然越低。所以债券的收益率与价格是反向的。这种方向关系和其它所有资产都不同。任何其它资产,股票、房地产等,一定是价格越涨(跌),收益率越高(低),二者同向变化。唯独债券的价格与收益率是反向关系。如果你把一张普通固息债的价格与收益率作图,则能明显看到二者的反向关系而不是正向关系。
但如果想要彻底理解“债券价格与收益率反向变化”这一点,不要用数学的“分母越大分子不变则商越小”来说服自己、也不要用这张图来说服自己。小学生也看得懂分数、看得懂图,只理解数学逻辑不是真理解,用业务逻辑说服自己才是真理解。
这个反向关系的业务逻辑就是:因为债券的现金流收入是提前约定的,好比一块饼的大小已经固定了,成本就是100元。那么你用90元买它,和用10元买它,哪个收益率高?当然是10元。所以,因为收入确定,所以成本价格越低,收益率越高,反之亦然。所以用不严谨但是易于理解的方式来说,债券是‘先收益后成本’,即先确定了收益,再去算成本。而其它资产是‘先成本后收益’,比如现定了500万成本买这套房,看以后涨跌到多少再算收益率。这也是为什么债券的收益率下行(收益率通常不说上涨下跌,而说上行下行),使得债券价格上涨,我们称为债券牛市,反之亦然。
所以我们强调,数学只是工具,业务才是目的。归根结底,金融是社会科学,不是自然科学。不管使用的计算工具再怎么复杂高深,也不是我们研究的目的本身,我们的目的是研究金融这种人的社会行为,所以一定要能从业务本身理解,而非局限于计算逻辑。
债券定价公式里,面值、票息都是已知的,收益率是未知的、是自变量,价格是也是未知的、是因变量。所以债券价格的定价公式表达的是“债券价格是收益率的函数”,即债券价格随着收益率的变化而变化,反之亦然。
综上所述,完整严谨地说,债券的到期收益率YTM是假设双方平安无事到期年化平均复利回报率。
5、YTM与实际持有期回报率
不要把YTM和实际持有期回报率混为一谈。YTM是假设的某一时点直至持有到期能实现的年化收益率,是一个假设收益率。实际持有期回报率是指这只债买入卖出期间的实际回报率。如果持有人在到期前将债券卖出,那么从买入到卖出的期间回报率,须根据年化后的买卖价差进行计算,得到期间的年化复利回报率。如果债券持有人真的顺利持有至到期了、并且将每期票息的投资回报率做到了YTM,那么YTM才等于实际持有期回报率。
久期
黑鸡的加权平均时间是5.5天,黄鸡是8.2632天,黑鸡还是赢了。
黄鸡要怎么赢呢?把大蛋下到第一天,平均每个蛋就是4.9517天,就能赢。
这种加权平均的思维方式,就是麦氏久期,是一个加拿大经济学家麦考利发明的,它衡量的是一只债券每笔现金流的加权平均回本时间(注意是平均而不是加总)。债券的每期现金流就好比每个鸡蛋。
注意:
- 麦氏久期是每笔现金流的回本平均时间,不是总时间,即债券的加权平均剩余期限。
- 麦氏久期是有单位的,一般是年。我们平时说的拉长久期、缩短久期,都是说的麦氏久期。
- 随着债券价格、收益率的波动、剩余期限的逐日缩短,麦氏久期也会随之变化。价格、收益率变化一次,久期就马上跟随变化。
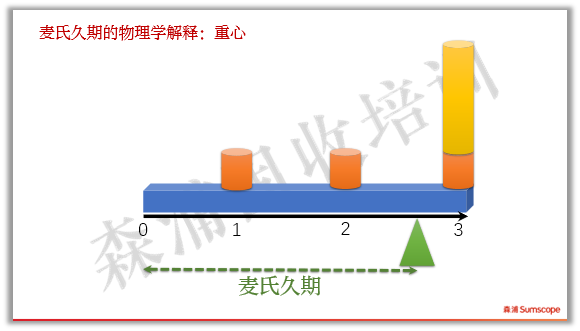
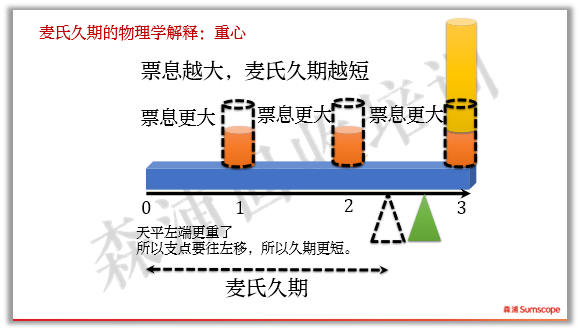
我们还可以用物理模型来解释麦氏久期:如果现金流换成砝码,时间轴换成天平(注意忽略天平横杠本身的重量,只考虑砝码重量),那么麦氏久期就是能使天平平衡时,左端到支点的长度。如下图:
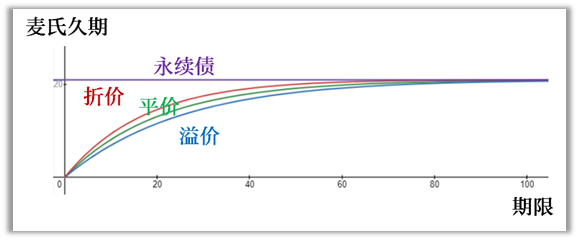
如果其他条件不变,票息变大,支点必须左移,那么麦氏久期越短。
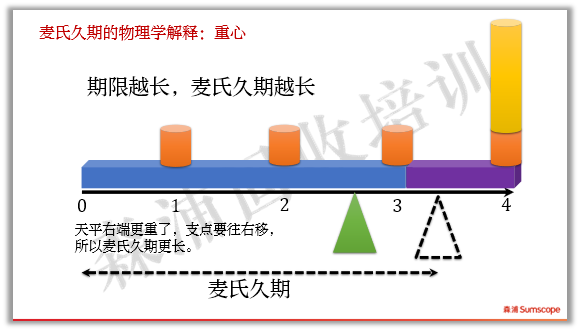
如果期限增加,麦氏久期越长。
对于无息债,因为两边都没有砝码,所以麦氏久期就等于其期限。反过来说,一个麦氏久期为2.9125的多笔现金流债券,平均回本时间就相当于一只2.9125年的零息债。
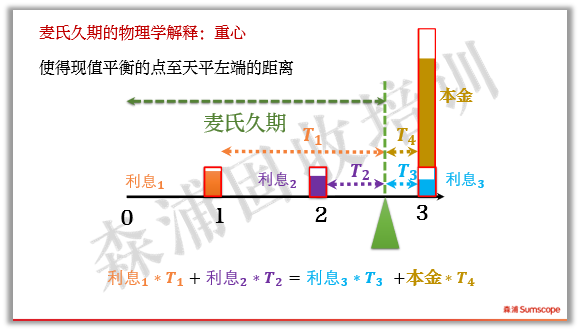
这个解释不仅在物理上是直观的,在数学上也是精确的。如下图,用贴现后的现值作为砝码重量计算天平两边的力矩,刚好相等。
现金流越早,回本时间越短。现金流越大,回本也越短。所以,投资者用麦氏久期来衡量债券风险高低时,就是现金流早比晚好、大比小好。
在其它资产中,也有类似的回本时间的概念,比如股票的市盈率、房地产的租售比。股票静态市盈率衡量的是股价等于多少倍的年度盈利,也就是投资者靠盈利回报能多少年收回买股票的成本。房屋租售比是月租金比房价,那么租售比乘以12之后求倒数,就是靠租金需要多少年回本。当然,严格来说,股票市盈率不能算现金型回本指标,因为盈利并不一定都分给股东,这里只是供大家拓宽思路,跳出固收看固收。
修正久期
麦氏久期仅仅是个回本平均时间指标,它并没有揭示除此之外的任何其它特征。如果债券价格波动,如何度量它的风险呢?之前我们说过,债券的价格公式是价格与收益率的函数。收益率动,价格就动。于是经济学家们开始思考:如果债券收益率波动一个单位,债券价格波动多少个单位呢?
把债券价格公式进行一般化,P是债券价格,YTM是收益率,C、F、n是已知的票息、面值、期限。
我们关心的其实就是“自变量x变化一个单位数值,因变量y变化多少百分比”的问题。我们已经有很成熟的方法来解决“x变化一个单位数值时y变化几个单位数值”这个问题,即求导数。对以上公式,求P对YTM的一阶导数:
注意只是算出来了当YTM变化一个微小单位时P变化的数值,我们需要度量的是变化幅度或者说百分比,而不仅仅是数值。所以要将两边同时除以P,然后再提取公因子,得到:
左边红色部分就是债券价格对收益率变化的敏感度。无巧不成书,右边的蓝色部分恰好就是麦氏久期,负号表示的是价格和收益率变化的反向关系。
由于这个数学关系,可以通过麦氏久期进行数学修正而得到,在数值上是修正的麦氏久期,所以债券价格对收益率变化的敏感度被称为修正久期,但其实际业务出发点已经不是回本时间了,尽管数值上是接近麦氏久期的,那也只是一种数学巧合。所以尽管业内都已普遍接受修正久期这个名字,但如果把它更名为价格收益率弹性、敏感度,更名副其实。
一年付息一次的固息债的修正久期,等于麦氏久期除以1+YTM。如果是付息m次的固息债,那么等于麦氏久期除以1+YTM/m。如果m是无穷次,意味着连续付息,那么YTM/m趋向于0,麦氏久期就等于修正久期了。
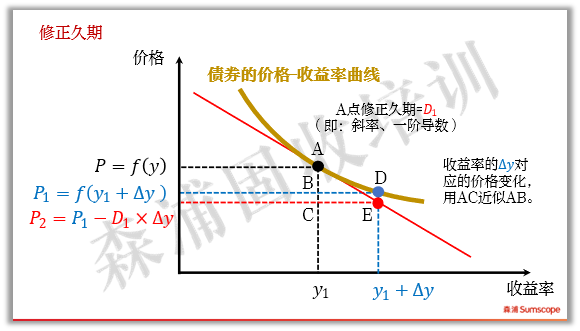
我们再来看数学的作图解释。从价格收益率曲线上看,修正久期是曲线的一阶导数,即用直线去替代曲线来度量价格对于收益率变化的变化。例如下图,当收益率从y1变化到y1+△y时,曲线从A点下滑到D点,债券价格从A下跌到B,但直接计算AB很不方便,我们用AC去近似AB。AC即修正久期。显然,收益率变化幅度小时,切线和曲线很接近,近似效果较好。当收益率变化很大,则修正久期的近似效果越差,这时就要用到进一步的近似工具:凸性。后续凸性章节将专门介绍。
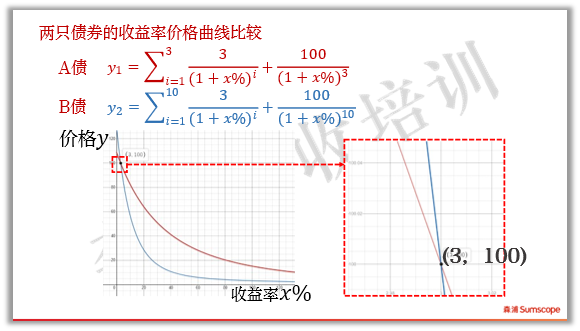
我们来看看两只不同债券的修正久期差异。假设有两只债券,票息率都是3%,A债期限3年,B债期限10年,债券的价格-收益率曲线如下图:
两只债的价格-收益率曲线在收益率3%处相交。因为票息是3%,当X轴的收益率为3%时,Y轴价格等于面值100。
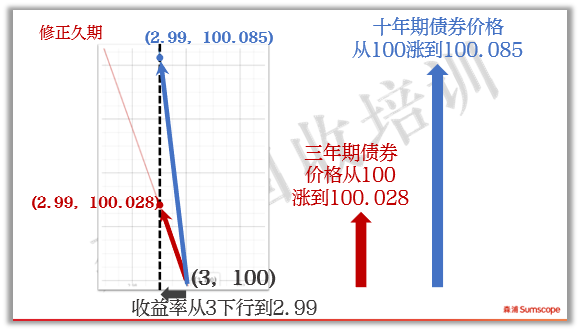
当两只债的收益率从3%下行1个BP到2.99%时,三年期债的价格上涨到100.028元,而十年期债券价格上涨到100.085,显然十年期债的价格上涨更多。这从二者的曲线上也能看出来。
注意:
- 修正久期与麦氏久期数值接近,拥有类似特点:其它条件不变时,修正久期与期限成正比,与票息、收益率成反比。如果一时回忆不起来了,那就用前面讲过的天平模型去推理。
- 价格与修正久期的快速计算:如果修正久期是X,那么当收益率上行(下行)1个BP时,价格下跌(上涨)约万分之X(即0.0X%)。比如假设十年国债修正久期为8.3,那么收益率下行1个BP时,价格上升约万分之8.3,1000万市值则上涨8300元,反之亦然。这个8300元,即收益率变化1个BP时债券价格变化的金额,称之为PVBP或者DV01。PBVP是Price Value per 1BP的缩写。DV01是Dollar Value per 1BP的简称,因为美元最通用所以形成了国际惯例成为Dollar而已,不用纠结为啥不是RMB。
- 修正久期是个百分比、万分比的幅度概念,只有高低大小,所以没有单位,不可以说修正久期是多少年。
- 当收益率变化幅度大时,修正久期的近似效果越差。
因为期限越长,久期越大。那么当债券牛市来临,如果投资者认为长债、短债的收益率都将下行同样幅度,那么投资者倾向于将持有的债券换成长期限债券,获得更大的久期,这样将获得更高的盈利,类似于高速公路开车就要挂高档。反之,熊市来临,如果投资者认为长债、短债的收益率都将上行同样幅度,那么投资者倾向于将持有的债券换成短期限债券,获得更小的久期,这样将获得更低的亏损,类似于崎岖小路开车就要挂中低档。这就是所谓的“牛市加久期、熊市减久期”。这里说的久期,并不特指麦氏久期或修正久期。不过,今后我们将学习到,这个牛熊市加减久期的口诀并不绝对成立,还要考虑长短端的上下行幅度、收益率的波动率大小等。
期限、久期的关系
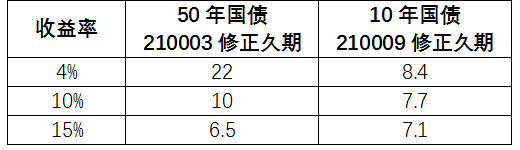
期限越长,久期对于收益率变化的敏感度就越高(提示:这种敏感度就是后面我们将讲到的凸性)。请看下表。
收益率从4%上行到10%再到15%,50年国债的久期变化幅度明显大于10年国债。甚至当收益率上行到15%时,50年国债的修正久期比10年国债的还要低!虽然根据历史经验,如此大的收益率变化幅度基本不可能发生,但举这个例子是为了让各位加深印象:久期的实际值和实际变化,需要实事求是地计算,切忌只根据剩余期限的长短而想当然。
凸性
由于久期只能实现对债券的线性(切线)近似,如果想提高近似效果,就要用到凸性来实现二次方近似了,也就是价格对收益率的二阶导数、“久期的久期”:当收益率变化一个单位时,久期的变化幅度。
对于凸性的特点,我们总结为“久期是双刃剑,凸性是心头好”。也就是说,凸性是投资者非常喜欢的一种特点。因为当收益率下行上行相同幅度时,凸性大的债券价格涨得多跌得少。
单从数值上看,虽然凸性的增长比久期要快很多,但是由于其对债券价格的影响是二阶的而不是一阶的,所以对债券价格的影响,久期仍然是一阶的、影响力最大的,凸性是二阶的、影响力其次的。
转
https://mp.weixin.qq.com/s/HQ1KtAj1uMrqxiYGhVgZIw